Cardinality of real numbers and set of real numbers between 0 and 1

Question : Show that the set of all real numbers has the same cardinality as the set of real number between 0 and 1.

Solution : Solution Let S be the open interval of real numbers between 0 and 1

S={x  ∈ R| 0 < x < 1 }.

Imagine picking up S and bending it into circle as shown below. Since S does not include either endpoint 0 or 1, the top-most point of the circle is omitted from the drawing.

 

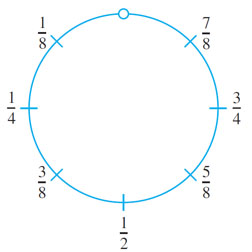
Define a function F: S→R as follows: Draw a number line and place the interval, S, somewhat enlarged and bent into a circle tangent to the line above the point 0. This is shown below.

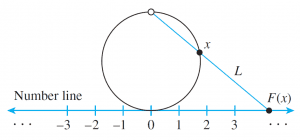
For each point x on the circle representing S, draw a straight line L through the top-most point of the circle x. Let F(x) be the point of intersection of L and the number line. F(x) is called the projection of x onto the number line.

It is clear from the geometry of the situation that distinct point on the circle go to distinct point on the number line, so F is one-to-one. In addition, given any point y on the number line, a line can be drawn through y and the top-most point of the circle. This line must intersect the circle at some point x, and, by definition, y=F(x). Thus F is onto. Hence F is a one-to-one correspondence from S to R, and so S and R have the same cardinality.